Become an expert in Computational Fluid Mechanics Techniques in just a few months"

Within Simulation we find different computer techniques such as Computational Fluid Dynamics, which has become very important nowadays due to its multiple advantages, such as the level of detail it provides, the time saving or the cost reduction. Its different procedures simulate by means of numerical methods the real behavior of the fluids, with the objective of obtaining more information and understanding of the same. Therefore, they are applicable in multiple areas such as aerospace, automotive, environment, biomedicine or wind energy.

To get the most out of these techniques, advanced knowledge is required, which is increasingly in demand in the labor market, which is why TECH has designed a Postgraduate diploma in CFD Techniques. This program aims to provide students with a good specialized base in the different numerical methods of CFD, so that they can face their work in this field, with the highest quality in their work.

In this way, content has been created that delves into Fluid Mechanics, High Performance Computing, Advanced Mathematics for CFD, Finite Volume Methods and Advanced Methods for CFD, among other relevant topics.

All this through a 100% online content that gives the student total freedom to organize their studies and schedules as best suits them, being able to combine the completion of the program with their other daily activities. In addition, the student will be provided with dynamic multimedia materials, practical exercises, fully updated information and the latest teaching technologies.

Delve into essential CFD Techniques and master an area with brilliant job potential"

This Postgraduate diploma in CFD Techniques contains the most complete and up-to-date program on the market. The most important features include:

• The development of case studies presented by experts in CFD Techniques
• The graphic, schematic, and practical contents with which they are created, provide scientific and practical information on the disciplines that are essential for professional practice
• Practical exercises where self-assessment can be used to improve learning
• Its special emphasis on innovative methodologies
• Theoretical lessons, questions to the expert, debate forums on controversial topics, and individual reflection assignments
• Content that is accessible from any fixed or portable device with an Internet connection

Acquire new knowledge and improved skills in Finite Element Methods or Smoothed Particle Hydrodynamics"

The program’s teaching staff includes professionals from sector who contribute their work experience to this educational program, as well as renowned specialists from leading societies and prestigious universities.

Its multimedia content, developed with the latest educational technology, will provide the professional with situated and contextual learning, i.e., a simulated environment that will provide an immersive education programmed to learn in real situations.

The design of this program focuses on Problem-Based Learning, by means of which the professional must try to solve the different professional practice situations that are presented throughout the academic course. For this purpose, the student will be assisted by an innovative interactive video system created by renowned experts.

Enroll now and get access to all SPH-based Simulator Development content"

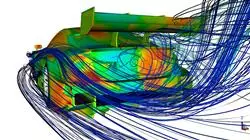
Enjoy the best theoretical and practical content in Advanced Methods for CFD"

The structure and content of this program have been meticulously created by the professionals in CFD Techniques that make up TECH's team of subject matter experts. In this way, they have resulted in accurate multimedia materials, verified and updated information, as well as the most useful practical activities to test the new skills acquired by the students.

Quality content designed under the most efficient pedagogical methodology, Relearning, in which TECH is a pioneer"

Module 1. Fluid Mechanics and High-Performance Computing

1.1. Dynamics of computational fluid mechanics

1.1.1. The origin of the turbulence
1.1.2. The need for modeling
1.1.3. CFD work process

1.2. The Equations of Fluid Mechanics

1.2.1. The continuity equation
1.2.2. The Navier-Stokes equation
1.2.3. The energy equation
1.2.4. The Reynolds averaged equations

1.3. The problem of closing equations

1.3.1. The Bousinesq hypothesis
1.3.2. Turbulent viscosity in a spray
1.3.3. CFD Modeling

1.4. Dimensionless numbers and dynamic similarity

1.4.1. Dimensionless numbers in fluid mechanics
1.4.2. The principle of dynamic similarity
1.4.3. Practical example: wind tunnel modeling

1.5. Turbulence Modeling

1.5.1. Direct numerical simulations
1.5.2. Simulations of large eddies
1.5.3. RANS Methods
1.5.4. Other Methods

1.6. Experimental Techniques

1.6.1. PIV
1.6.2. Hot wire
1.6.3. Wind and water tunnels

1.7. Supercomputing environments

1.7.1. Supercomputing. Ide future
1.7.2. Supercomputer operation
1.7.3. Tools for use

1.8. Software in parallel architectures

1.8.1. Distributed environments: MPI
1.8.2. Shared memory: GPU
1.8.3. Data engraving: HDF5

1.9. Grid computing

1.9.1. Description of computer farms
1.9.2. Parametric problems
1.9.3. Queuing systems in grid computing

1.10. GPU, the future of CFD

1.10.1. GPU Environments
1.10.2. GPU Programming
1.10.3. Practical example: artificial intelligence in fluids using GPUs

Module 2. Advanced mathematics for CFD

2.1. Fundamentals of Mathematics

2.1.1. Gradients, divergences and rotations. Total derivative
2.1.2. Ordinary Differential Equations
2.1.3. Partial derivative equations

2.2. Statistics

2.2.1. Averages and moments
2.2.2. Probability density functions
2.2.3. Correlation and energy spectra

2.3. Strong and weak solutions of a differential equation

2.3.1. Function bases. Strong and weak solutions
2.3.2. The finite volume method. The heat equation
2.3.3. The finite volume method. Navier-Stokes

2.4. Taylor's Theorem and Discretization in time and space

2.4.1. Finite differences in 1 dimension. Error order
2.4.2. Finite differences in 2 dimensions
2.4.3. From continuous equations to algebraic equations

2.5. Algebraic problem solving, LU method

2.5.1. Algebraic problem solving methods
2.5.2. The LU method on full matrices
2.5.3. The LU method in sparse matrices

2.6. Algebraic Problem Solving, Iterative Methods I

2.6.1. Iterative methods. Waste
2.6.2. Jacobi's method
2.6.3. Generalization of Jacobi's method

2.7. Algebraic problem solving, iterative methods II

2.7.1. Multi-grid methods: V-cycle: interpolation
2.7.2. Multi-grid methods: V-cycle: extrapolation
2.7.3. Multi-grid methods: W-cycle
2.7.4. Error estimation

2.8. Eigenvalues and eigenvectors

2.8.1. The algebraic problem
2.8.2. Application to the heat equation
2.8.3. Stability of differential equations

2.9. Non-linear evolution equations

2.9.1. Heat equation: explicit methods
2.9.2. Heat equation: implicit methods
2.9.3. Heat equation: Runge-Kutta methods

2.10. Stationary non-linear equations

2.10.1. The Newton-Raphson method
2.10.2. 1D Applications
2.10.3. 2D Applications

Module 3. CFD in Application Environments: Finite Volumes Methods

3.1. Finite Volume Methods

3.1.1. Definitions in FVM
3.1.2. Historical Background
3.1.3. MVF in Structures

3.2. Source Terms

3.2.1. External volumetric forces

3.2.1.1. Gravity, centrifugal force

3.2.2. Volumetric (mass) and pressure source term (evaporation, cavitation, chemical)
3.2.3. Scalar source term

3.2.3.1. Temperature, species

3.3. Applications of boundary conditions

3.3.1. Input and Output
3.3.2. Symmetry condition
3.3.3. Wall condition

3.3.3.1. Tax values
3.3.3.2. Values to be solved by parallel calculation
3.3.3.3. Wall models

3.4. Boundary Conditions

3.4.1. Known boundary conditions: Dirichlet

3.4.1.1. Scalars
3.4.1.2. Diseases

3.4.2. Boundary conditions with known derivative: Neumann

3.4.2.1. Zero gradient
3.4.2.2. Finite gradient

3.4.3. Cyclic boundary conditions: Born-von Karman
3.4.4. Other boundary conditions: Robin

3.5. Temporary integration

3.5.1. Explicit and implicit Euler
3.5.2. Lax-Wendroff time step and variants (Richtmyer and MacCormack)
3.5.3. Runge-Kutta multi-stage time step

3.6. Upwind Schematics

3.6.1. Riemman's Problem
3.6.2. Main upwind schemes: MUSCL, Van Leer, Roe, AUSM
3.6.3. Design of an upwind spatial scheme

3.7. High order schemes

3.7.1. High-order discontinuous Galerkin
3.7.2. ENO and WENO
3.7.3. High Order Schemes. Advantages and Disadvantages

3.8. Pressure-velocity convergence loop

3.8.1. PISO
3.8.2. SIMPLE, SIMPLER and SIMPLEC
3.8.3. PIMPLE
3.8.4. Transient loops

3.9. Moving contours

3.9.1. Overlocking techniques
3.9.2. Mapping: mobile reference system
3.9.3. Immersed boundary method
3.9.4. Overlapping meshes

3.10. Errors and uncertainties in CFD modeling

3.10.1. Precision and accuracy
3.10.2. Numerical errors
3.10.3. Input and physical model uncertainties

Module 4. Advanced Methods for CFD

4.1. Finite Element Method (FEM)

4.1.1. Domain discretization. Finite Elements
4.1.2. Form functions. Reconstruction of the continuous field
4.1.3. Assembly of the coefficient matrix and boundary conditions
4.1.4. Solving Systems of Equations

4.2. FEM: case study. Development of a FEM simulator

4.2.1. Form functions
4.2.2. Assembling the coefficient matrix and applying boundary conditions
4.2.3. Solving Systems of Equations
4.2.4. Post-Process

4.3. Smoothed Particle Hydrodynamics (SPH)

4.3.1. Fluid field mapping from particle values
4.3.2. Evaluation of derivatives and particle interaction
4.3.3. The smoothing function. The kernel
4.3.4. Boundary Conditions

4.4. SPH: development of a simulator based on SPH

4.4.1. The kernel
4.4.2. Storage and sorting of particles in voxels
4.4.3. Development of boundary conditions
4.4.4. Post-Process

4.5. Direct Simulation Monte Carlo (DSMC)

4.5.1. Kinetic-molecular theory
4.5.2. Statistical mechanics
4.5.3. Molecular equilibrium

4.6. DSMC: methodology

4.6.1. Applicability of the DSMC method
4.6.2. Modeling
4.6.3. Considerations for the applicability of the method

4.7. DSMC: applications

4.7.1. Example in 0-D: thermal relaxation
4.7.2. 1-D example: normal shock wave
4.7.3. 2-D example: supersonic cylinder
4.7.4. 3-D example: supersonic corner
4.7.5. Complex example: space Shuttle

4.8. Lattice-Boltzmann Method (LBM)

4.8.1. Boltzmann equation and equilibrium distribution
4.8.2. De Boltzmann a Navier-Stokes. Chapman-Enskog Expansion
4.8.3. From probabilistic distribution to physical magnitude
4.8.4. Conversion of units. From physical quantities to lattice quantities

4.9. LBM: Numerical approximation

4.9.1. The LBM algorithm. Transfer step and collision step
4.9.2. Collision operators and momentum normalization
4.9.3. Boundary Conditions

4.10. LBM: case study

4.10.1. Development of a simulator based on LBM
4.10.2. Experimentation with various collision operators
4.10.3. Experimentation with various turbulence models

The world's best online university offers you a tailor-made program to quickly excel in the field of Computational Fluid Dynamics"