ИИ в клинической практике обещает повысить качество медицинского обслуживания, уменьшить количество ошибок и открыть новые горизонты для персонализированной медицины и биомедицинских исследований" 

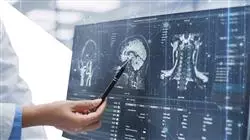
Искусственный интеллект можно применять в медицинской практике, анализируя большие массивы медицинских данных для выявления закономерностей и тенденций и способствуя более ранней и точной постановке диагноза. Кроме того, при ведении пациентов ИИ способен предвидеть возможные осложнения, персонализировать лечение и оптимизировать распределение ресурсов, повышая эффективность и качество медицинской помощи. Автоматизация рутинных задач также высвобождает время специалистов, позволяя им сосредоточиться на более сложных и гуманных аспектах ухода, что способствует значительному прогрессу в медицине. 

По этой причине TECH разработал эту Специализированную магистратуру в области искусственного интеллекта в клинической практике с комплексным и специализированным подходом. Конкретные модули будут включать в себя широкий спектр вопросов: от освоения практических инструментов искусственного интеллекта до критического понимания его этического и правового применения в медицине. Упор на конкретные медицинские приложения, такие как диагностика с помощью ИИ и обезболивание, позволит специалистам получить передовые навыки и знания в ключевых областях здравоохранения. 

Также будет поощряться междисциплинарное сотрудничество, что подготовит студентов к работе в различных командах в клинических условиях. Кроме того, этический, правовой и управленческий подход обеспечит ответственное понимание и практическое применение при разработке и внедрении решений ИИ в здравоохранении. Сочетание теоретического и практического обучения, а также применение больших данных в здравоохранении позволят врачам комплексно и компетентно решать текущие и будущие задачи в этой области. 

Таким образом, TECH разработал полную программу, основанную на инновационной методологии Relearning, для подготовки высококвалифицированных специалистов в области искусственного интеллекта. При такой форме обучения основное внимание уделяется повторению ключевых понятий для обеспечения их прочного понимания. Для доступа к материалам в любое время потребуется только электронное устройство с подключением к Интернету, что освобождает студентов от фиксированного расписания или необходимости лично присутствовать на занятиях. 

Структура программы, построенная на модулях, позволит вам последовательно пройти путь от основ до самого продвинутого применения ИИ" 

Данная Специализированная магистратура в области искусственного интеллекта в клинической практике содержит самую полную и современную научную программу на рынке. Наиболее характерными особенностями обучения являются:

• Разбор практических кейсов, представленных экспертами в области искусственного интеллекта в клинической практике 
• Наглядное, схематичное и исключительно практичное содержание курса предоставляет научную и практическую информацию по тем дисциплинам, которые необходимы для осуществления профессиональной деятельности 
• Практические упражнения для самооценки, контроля и улучшения успеваемости 
• Особое внимание уделяется инновационным методологиям 
• Теоретические занятия, вопросы эксперту, дискуссионные форумы по спорным темам и самостоятельная работа 
• Учебные материалы курса доступны с любого стационарного или мобильного устройства с выходом в интернет 

Вы погрузитесь в науку о медицинских данных с поддержкой искусственного интеллекта, изучите биостатистику и аналитику больших данных благодаря 2700 часам инновационныъ материалов" 

В преподавательский состав программы входят профессионалы из отрасли, которые привносят в обучение опыт своей работы, а также признанные специалисты из ведущих сообществ и престижных университетов. 

Мультимедийное содержание программы, разработанное с использованием новейших образовательных технологий, позволит специалисту проходить обучение с учетом контекста и ситуации, т.е. в симулированной среде, обеспечивающей иммерсивный учебный процесс, запрограммированный на обучение в реальных ситуациях. 

Структура этой программы основана на проблемно-ориентированном обучении, с помощью которого специалист должен попытаться разрешать различные ситуации из профессиональной практики, возникающие в течение учебного курса. В этом специалистам поможет инновационная интерактивная видеосистема, созданная признанными экспертами. 

Благодаря этой 100% онлайн-программе вы сможете проанализировать, как искусственный интеллект интерпретирует генетические данные для разработки конкретных терапевтических стратегий"

Вы будете применять методы интеллектуального анализа данных и машинного обучения в контексте здравоохранения. Чего вы ждете, чтобы поступить?"

Данная Специализированная магистратура тщательно разработана, чтобы объединить клиническое мастерство с технологическими инновациями. Ее структура основана на специализированных модулях, начиная с основ искусственного интеллекта и заканчивая конкретными применениями в медицинской среде. Таким образом, в программе будет соблюден идеальный баланс между передовой теорией и практическим применением, что позволит специалистам решать любые задачи — от анализа данных до персонализации лечения. Таким образом, студенты подготовлены к тому, чтобы изменить медицину к лучшему, обладая прогрессивным видением и прочными техническими навыками. 

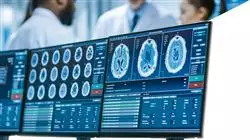
Обновите свою ежедневную клиническую практику, чтобы быть в курсе технологической революции в здравоохранении и внести свой вклад в развитие клинической практики" 

Модуль 1. Основы искусственного интеллекта

1.1. История искусственного интеллекта 

1.1.1. Когда мы начали говорить об искусственном интеллекте?
1.1.2. Упоминания в кино 
1.1.3. Важность искусственного интеллекта 
1.1.4. Технологии, обеспечивающие и поддерживающие искусственный интеллект 

1.2. Искусственный интеллект в играх 

1.2.1. Теория игр 
1.2.2. Минимакс и Альфа-бета-отсечение 
1.2.3. Моделирование: Монте-Карло 

1.3. Нейронные сети 

1.3.1. Биологические основы 
1.3.2. Вычислительная модель 
1.3.3. Контролируемые и неконтролируемые нейронные сети 
1.3.4. Простой перцептрон 
1.3.5. Многослойный перцептрон 

1.4. Генетические алгоритмы 

1.4.1. История 
1.4.2. Биологическая основа 
1.4.3. Кодирование проблемы 
1.4.4. Генерация начальной популяции 
1.4.5. Основной алгоритм и генетические операторы 
1.4.6. Оценка отдельных лиц: Fitness 

1.5. Тезаурусы, словари, таксономии 

1.5.1. Словари 
1.5.2. Таксономия 
1.5.3. Тезаурусы 
1.5.4. Онтологии 
1.5.5. Представление знаний: семантическая паутина 

1.6. Семантическая паутина 

1.6.1. Спецификация: RDF, RDFS и OWL 
1.6.2. Выводы/рассуждения 
1.6.3. Linked Data 

1.7. Экспертные системы и DSS 

1.7.1. Экспертные системы 
1.7.2. Системы поддержки принятия решений 

1.8. Чатботы и виртуальные помощники

1.8.1. Типы помощников: голосовые и текстовые помощники
1.8.2. Основополагающие детали для развития помощника: Намерения, структура и диалог 
1.8.3. Интеграция: web, Slack, Whatsapp, Facebook 
1.8.4. Инструменты разработки помощников: Dialog Flow, Watson Assistant

1.9. Стратегия и внедрение ИИ 
1.10. Будущее искусственного интеллекта

1.10.1. Мы понимаем, как определять эмоции с помощью алгоритмов
1.10.2. Создание личности: язык, выражения и содержание
1.10.3. Тенденции искусственного интеллекта
1.10.4. Размышления

Модуль 2. Виды и жизненный цикл данных 

2.1. Статистика

2.1.1. Статистика: описательная статистика, статистические выводы
2.1.2. Население, выборка, индивидуум
2.1.3. Переменные: определение, шкалы измерения

2.2. Типы статистических данных

2.2.1. По типу

2.2.1.1. Количественные: непрерывные данные и дискретные данные
2.2.1.2. Качественные: биномиальные данные, номинальные данные, порядковые данные 

2.2.2. По форме 

2.2.2.1. Числовые
2.2.2.2. Текст 
2.2.2.3. Логические

2.2.3. Согласно источнику

2.2.3.1. Первичные
2.2.3.2. Вторичные

2.3. Жизненный цикл данных

2.3.1. Этапы цикла
2.3.2. Основные этапы цикла
2.3.3. Принципы FAIR

2.4. Начальные этапы цикла

2.4.1. Определение целей
2.4.2. Определение необходимых ресурсов
2.4.3. Диаграмма Гантта
2.4.4. Структура данных

2.5. Сбор данных

2.5.1. Методология сбора
2.5.2. Инструменты сбора
2.5.3. Каналы сбора

2.6. Очистка данных

2.6.1. Этапы очистки данных
2.6.2. Качество данных
2.6.3. Работа с данными (с помощью R)

2.7. Анализ данных, интерпретация и оценка результатов

2.7.1. Статистические меры
2.7.2. Индексы отношений
2.7.3. Добыча данных

2.8. Хранилище данных (datawarehouse)

2.8.1. Элементы, входящие в его состав
2.8.2. Разработка
2.8.3. Аспекты, которые следует учитывать

2.9. Доступность данных

2.9.1. Доступ
2.9.2. Полезность
2.9.3. Безопасность

2.10. Нормативно-правовые аспекты 

2.10.1. Закон о защите данных
2.10.2. Передовая практика
2.10.3. Другие нормативные аспекты

Модуль 3. Данные в искусственном интеллекте 

3.1. Наука о данных 

3.1.1. Наука о данных 
3.1.2. Передовые инструменты для исследователя данных 

3.2. Данные, информация и знания 

3.2.1. Данные, информация и знания
3.2.2. Типы данных 
3.2.3. Источники данных 

3.3. От данных к информации

3.3.1. Анализ данных 
3.3.2. Виды анализа 
3.3.3. Извлечение информации из набора данных 

3.4. Извлечение информации путем визуализации 

3.4.1. Визуализация как инструмент анализа 
3.4.2. Методы визуализации
3.4.3. Визуализация набора данных 

3.5. Качество данных 

3.5.1. Данные о качестве 
3.5.2. Очистка данных
3.5.3. Основная предварительная обработка данных 

3.6. Набор данных 

3.6.1. Обогащение набора данных 
3.6.2. Проклятие размерности 
3.6.3. Модификация нашего набора данных 

3.7. Выведение из равновесия

3.7.1. Дисбаланс классов 
3.7.2. Методы устранения дисбаланса 
3.7.3. Сбалансированность набора данных 

3.8. Модели без контроля

3.8.1. Модель без контроля 
3.8.2. Методы 
3.8.3. Классификация с помощью моделей без контроля 

3.9. Модели под контролем 

3.9.1. Модель под контролем 
3.9.2. Методы 
3.9.3. Классификация с помощью моделей под контролем 

3.10. Инструменты и передовой опыт 

3.10.1. Передовая практика для специалиста по исследованию данных 
3.10.2. Лучшая модель
3.10.3. Полезные инструменты 

Модуль 4. Добыча данных. Отбор, предварительная обработка и преобразование 

4.1. Статистический вывод 

4.1.1. Описательная статистика vs. Статистическое заключение 
4.1.2. Параметрические методы 
4.1.3. Непараметрические методы 

4.2. Исследовательский анализ 

4.2.1. Описательный анализ
4.2.2. Визуализация 
4.2.3. Подготовка данных 

4.3. Подготовка данных 

4.3.1. Интеграция и очистка данных
4.3.2. Нормализация данных 
4.3.3. Преобразование данных

4.4. Отсутствующие данные 

4.4.1. Обработка отсутствующих значений 
4.4.2. Метод максимального правдоподобия 
4.4.3. Обработка отсутствующих данных в машинном обучении 

4.5. Шум в данных

4.5.1. Классы и признаки шума 
4.5.2. Фильтрация шумов
4.5.3. Шумовой эффект 

4.6. Проклятие размерности 

4.6.1. Oversampling 
4.6.2. Undersampling 
4.6.3. Редукция многомерных данных 

4.7. От непрерывных к дискретным признакам 

4.7.1. Непрерывные и дискретные данные 
4.7.2. Процесс дискретизации 

4.8. Данные

4.8.1. Выбор данных
4.8.2. Перспективы и критерии отбора 
4.8.3. Методы отбора

4.9. Выбор экземпляров 

4.9.1. Методы выбора экземпляра 
4.9.2. Выбор прототипов 
4.9.3. Расширенные методы выбора экземпляра 

4.10. Предварительная обработка больших данных 

Модуль 5. Алгоритм и сложность в искусственном интеллекте 

5.1. Введение в шаблоны разработки алгоритмов 

5.1.1. Рекурсия 
5.1.2. "Разделяй и властвуй" 
5.1.3. Другие стратегии 

5.2. Эффективность и анализ работы алгоритмов 

5.2.1. Меры эффективности 
5.2.2. Измерение объема данных на входе 
5.2.3. Измерение времени выполнения 
5.2.4. Случаи: худший, лучший и средний 
5.2.5. Асимптотическая нотация 
5.2.6. Критерии математического анализа нерекурсивных алгоритмов 
5.2.7. Критерии математического анализа рекурсивных алгоритмов 
5.2.8. Эмпирический анализ алгоритмов 

5.3. Алгоритмы сортировки 

5.3.1. Концепция сортировки 
5.3.2. Пузырьковая сортировка 
5.3.3. Сортировка выбором 
5.3.4. Сортировка вставками 
5.3.5. Сортировка слиянием (Merge_Sort) 
5.3.6. Быстрая сортировка (Quick_Sort) 

5.4. Алгоритмы с применением деревьев 

5.4.1. Концепция дерева 
5.4.2. Бинарные деревья 
5.4.3. Обходы деревьев 
5.4.4. Представление выражений 
5.4.5. Упорядоченные бинарные деревья 
5.4.6. Сбалансированные бинарные деревья 

5.5. Алгоритмы с применением кучей 

5.5.1. Что такое кучи 
5.5.2. Алгоритм сортировки кучей 
5.5.3. Очереди с приоритетом 

5.6. Алгоритмы на графах 

5.6.1. Представление 
5.6.2. Обход в ширину 
5.6.3. Обход в глубину 
5.6.4. Топологическая сортировка 

5.7. Жадные алгоритмы 

5.7.1. Жадная стратегия 
5.7.2. Элементы жадной стратегии 
5.7.3. Обмен монет 
5.7.4. Задача коммивояжера 
5.7.5. Задача о рюкзаке 

5.8. Поиск кратчайших путей 

5.8.1. Задача о кратчайшем пути 
5.8.2. Отрицательные дуги и циклы 
5.8.3. Алгоритм Дейкстры 

5.9. Жадные алгоритмы на графах 

5.9.1. Минимальное остовное дерево 
5.9.2. Алгоритм Прима 
5.9.3. Алгоритм Краскала 
5.9.4. Анализ сложности 

5.10. Техника Backtracking 

5.10.1. Техника Backtracking 
5.10.2. Альтернативные техники 

Модуль 6. Интеллектуальные системы 

6.1. Теория агентов 

6.1.1. История концепции 
6.1.2. Определение агента 
6.1.3. Агенты в системах искусственного интеллекта 
6.1.4. Агенты в программной инженерии 

6.2. Архитектуры агентов 

6.2.1. Процесс рассуждения агента 
6.2.2. Реактивные агенты 
6.2.3. Дедуктивные агенты 
6.2.4. Гибридные агенты 
6.2.5. Сравнение 

6.3. Информация и знания 

6.3.1. Различие между данными, информацией и знаниями 
6.3.2. Оценка качества данных 
6.3.3. Методы сбора данных 
6.3.4. Методы получения информации 
6.3.5. Методы приобретения знаний 

6.4. Представление знаний 

6.4.1. Важность представления знаний 
6.4.2. Определение представления знаний через их роли 
6.4.3. Характеристики представления знаний 

6.5. Онтологии 

6.5.1. Введение в метаданные 
6.5.2. Философская концепция онтологии 
6.5.3. Вычислительная концепция онтологии 
6.5.4. Онтологии доменов и онтологии более высокого уровня 
6.5.5. Как создать онтологию? 

6.6. Онтологические языки и программное обеспечение для создания онтологий 

6.6.1. Семантическая тройка RDF, Turtle и N 
6.6.2. RDF Schema 
6.6.3. OWL 
6.6.4. SPARQL 
6.6.5. Знакомство с различными инструментами для создания онтологий 
6.6.6. Установка и использование Protégé 

6.7. Семантическая паутина 

6.7.1. Текущее состояние и будущее семантической паутины 
6.7.2. Семантические веб-приложения 

6.8. Другие модели представления знаний 

6.8.1. Словари 
6.8.2. Обзор 
6.8.3. Таксономия 
6.8.4. Тезаурусы 
6.8.5. Фолксономии 
6.8.6. Сравнение 
6.8.7. Карты разума 

6.9. Оценка и интеграция представлений знаний 

6.9.1. Логика нулевого порядка 
6.9.2. Логика первого порядка 
6.9.3. Дескрипционная логика 
6.9.4. Взаимосвязь между различными типами логики 
6.9.5. Пролог: программирование на основе логики первого порядка 

6.10. Семантические анализаторы, системы, основанные на знаниях, и экспертные системы 

6.10.1. Концепция анализатора 
6.10.2. Применение анализатора 
6.10.3. Системы, основанные на знаниях 
6.10.4. MYCIN, история экспертных систем 
6.10.5. Элементы и архитектура экспертных систем 
6.10.6. Создание экспертных систем 

Модуль 7. Машинное обучение и добыча данных 

7.1. Введение в процессы обнаружения знаний и основные концепции машинного обучения 

7.1.1. Ключевые понятия процесса обнаружения знаний 
7.1.2. Исторический взгляд процесса обнаружения знаний 
7.1.3. Этапы процесса обнаружения знаний 
7.1.4. Методы, используемые в процессах обнаружения знаний 
7.1.5. Характеристики хороших моделей машинного обучения 
7.1.6. Типы информации машинного обучения 
7.1.7. Основные концепции обучения 
7.1.8. Основные концепции обучения без контроля 

7.2. Исследование и предварительная обработка данных 

7.2.1. Обработка данных 
7.2.2. Обработка данных в потоке анализа данных 
7.2.3. Типы данных 
7.2.4. Преобразование данных 
7.2.5. Визуализация и исследование непрерывных переменных 
7.2.6. Визуализация и исследование категориальных переменных 
7.2.7. Корреляционные меры 
7.2.8. Наиболее распространенные графические представления 
7.2.9. Введение в многомерный анализ и снижение размерности 

7.3. Деревья решений 

7.3.1. Алгоритм ID 
7.3.2. Алгоритм C 
7.3.3. Перегрузка и обрезка 
7.3.4. Анализ результатов 

7.4. Оценка классификаторов 

7.4.1. Матрицы путаницы 
7.4.2. Матрицы численной оценки 
7.4.3. Kappa-статистика 
7.4.4. ROC-кривая 

7.5. Правила классификации 

7.5.1. Меры по оценке правил 
7.5.2. Введение в графическое представление 
7.5.3. Алгоритм последовательного оверлея 

7.6. Нейронные сети 

7.6.1. Основные понятия 
7.6.2. Простые нейронные сети 
7.6.3. Алгоритм Backpropagation 
7.6.4. Введение в рекуррентные нейронные сети 

7.7. Байесовские методы 

7.7.1. Основные понятия вероятности 
7.7.2. Теорема Байеса 
7.7.3. Наивный Байес 
7.7.4. Введение в байесовские сети 

7.8. Регрессия и модели непрерывного отклика 

7.8.1. Простая линейная регрессия 
7.8.2. Множественная линейная регрессия 
7.8.3. Логистическая регрессия 
7.8.4. Деревья регрессии 
7.8.5. Введение в машины опорных векторов (SVM) 
7.8.6. Меры соответствия 

7.9. Кластеризация 

7.9.1. Основные понятия 
7.9.2. Иерархическая кластеризация 
7.9.3. Вероятностные методы 
7.9.4. Алгоритм EM 
7.9.5. Метод B-Cubed 
7.9.6. Неявные методы 

7.10. Интеллектуальный анализ текста и обработка естественного языка (NLP) 

7.10.1. Основные понятия 
7.10.2. Создание корпуса 
7.10.3. Описательный анализ 
7.10.4. Введение в анализ чувств 

Модуль 8. Нейронные сети, основа глубокого обучения 

8.1. Глубокое обучение 

8.1.1. Виды глубокого обучения 
8.1.2. Области применения глубокого обучения 
8.1.3. Преимущества и недостатки глубокого обучения 

8.2. Операции 

8.2.1. Сумма 
8.2.2. Продукт 
8.2.3. Перевод 

8.3. Слои 

8.3.1. Входной слой 
8.3.2. Скрытый слой 
8.3.3. Выходной слой 

8.4. Склеивание слоев и операции 

8.4.1. Проектирование архитектур 
8.4.2. Соединение между слоями 
8.4.3. Распространение вперед 

8.5. Построение первой нейронной сети 

8.5.1. Проектирование сети 
8.5.2. Определение весов 
8.5.3. Практика сети 

8.6. Тренажер и оптимизатор 

8.6.1. Выбор оптимизатора 
8.6.2. Установление функции потерь 
8.6.3. Установление метрики 

8.7. Применение принципов нейронных сетей 

8.7.1. Функции активации 
8.7.2. Обратное распространение 
8.7.3. Установка параметров 

8.8. От биологических нейронов к искусственным 

8.8.1. Функционирование биологического нейрона 
8.8.2. Передача знаний искусственным нейронам 
8.8.3. Установление взаимоотношений между ними 

8.9. Реализация MLP (многослойного перцептрона) с помощью Keras 

8.9.1. Определение структуры сети 
8.9.2. Составление модели 
8.9.3. Обучение модели 

8.10. Тонкая настройка гиперпараметров нейронных сетей 

8.10.1. Выбор функции активации 
8.10.2. Установка скорости обучения 
8.10.3. Установка веса 

Модуль 9. Обучение глубоких нейронных сетей 

9.1. Градиентные задачи 

9.1.1. Методы оптимизации градиента 
9.1.2. Стохастические градиенты 
9.1.3. Методы инициализации весов 

9.2. Повторное использование предварительно обученных слоев 

9.2.1. Перенос результатов обучения 
9.2.2. Извлечение признаков 
9.2.3. Глубокое обучение 

9.3. Оптимизаторы 

9.3.1. Стохастические оптимизаторы градиентного спуска 
9.3.2. Оптимизаторы Adam и RMSprop 
9.3.3. Современные оптимизаторы 

9.4. Программирование скорости обучения 

9.4.1. Автоматическое управление скоростью обучения 
9.4.2. Циклы обучения 
9.4.3. Условия сглаживания 

9.5. Переоценка 

9.5.1. Перекрестная валидация 
9.5.2. Регуляризация 
9.5.3. Метрики оценки 

9.6. Практические рекомендации 

9.6.1. Конструкция модели 
9.6.2. Выбор метрик и параметров оценки 
9.6.3. Проверка гипотез 

9.7. Трансферное обучение 

9.7.1. Перенос результатов обучения 
9.7.2. Извлечение признаков 
9.7.3. Глубокое обучение 

9.8. Расширение данных 

9.8.1. Преобразования изображений 
9.8.2. Формирование синтетических данных 
9.8.3. Преобразование текста 

9.9. Практическое применение трансферного обучения 

9.9.1. Перенос результатов обучения 
9.9.2. Извлечение признаков 
9.9.3. Глубокое обучение 

9.10. Регуляризация 

9.10.1. L и L 
9.10.2. Регуляризация по принципу максимальной энтропии 
9.10.3. Dropout 

Модуль 10. Настройка моделей и обучение с помощью TensorFlow 

10.1. TensorFlow 

10.1.1. Использование библиотеки TensorFlow 
10.1.2. Обучение модели с помощью TensorFlow 
10.1.3. Операции с графиками в TensorFlow 

10.2. TensorFlow и NumPy 

10.2.1. Вычислительная среда NumPy для TensorFlow 
10.2.2. Использование массивов NumPy в TensorFlow 
10.2.3. Операции NumPy для графиков TensorFlow 

10.3. Настройка моделей и алгоритмов обучения 

10.3.1. Построение пользовательских моделей с помощью TensorFlow 
10.3.2. Управление параметрами обучения 
10.3.3. Использование методов оптимизации для обучения 

10.4. Функции и графики TensorFlow 

10.4.1. Функции в TensorFlow 
10.4.2. Использование графиков для обучения модели 
10.4.3. Оптимизация графов с помощью операций TensorFlow 

10.5. Загрузка и предварительная обработка данных с помощью TensorFlow 

10.5.1. Загрузка наборов данных с помощью TensorFlow 
10.5.2. Предварительная обработка данных с помощью TensorFlow 
10.5.3. Использование инструментов TensorFlow для манипулирования данными 

10.6. API tfdata 

10.6.1. Использование API tf.data для обработки данных 
10.6.2. Построение потоков данных с помощью tf.data 
10.6.3. Использование API tf.data для обучения моделей 

10.7. Формат TFRecord 

10.7.1. Использование API TFRecord для сериализации данных 
10.7.2. Загрузка файлов TFRecord с помощью TensorFlow 
10.7.3. Использование файлов TFRecord для обучения моделей 

10.8. Слои предварительной обработки в Keras 

10.8.1. Использование API предварительной обработки в Keras 
10.8.2. Построение pipelined предварительной обработки с помощью Keras 
10.8.3. Использование API предварительной обработки в Keras для обучения моделей 

10.9. Проект TensorFlow Datasets 

10.9.1. Использование TensorFlow Datasets для загрузки данных 
10.9.2. Предварительная обработка данных с помощью TensorFlow Datasets 
10.9.3. Использование TensorFlow Datasets для обучения моделей 

10.10. Построение приложения глубокого обучения с помощью TensorFlow 

10.10.1. Практическое применение 
10.10.2. Построение приложения глубокого обучения с помощью TensorFlow 
10.10.3. Обучение модели с помощью TensorFlow 
10.10.4. Использование приложения для прогнозирования результатов 

Модуль 11. Глубокое компьютерное зрение с использованием конволюционных нейронных сетей 

11.1. Архитектура Visual Cortex 

11.1.1. Функции зрительной коры 
11.1.2. Теории вычислительного зрения 
11.1.3. Модели обработки изображений 

11.2. Конволюционные слои 

11.2.1. Повторное использование весов в свертке 
11.2.2. Конволюция D 
11.2.3. Функции активации 

11.3. Слои кластеризации и реализация слоев кластеризации с помощью Keras 

11.3.1. Пулинг и стридинг 
11.3.2. Сплющивание 
11.3.3. Виды пулинга 

11.4. Архитектуры CNN 

11.4.1. Архитектура VGG 
11.4.2. Архитектура AlexNet 
11.4.3. Архитектура ResNet 

11.5. Реализация CNN ResNet - с использованием Keras 

11.5.1. Инициализация весов 
11.5.2. Определение входного слоя 
11.5.3. Определение выходного слоя 

11.6. Использование предварительно обученных моделей Keras 

11.6.1. Характеристики предварительно обученных моделей 
11.6.2. Использование предварительно обученных моделей 
11.6.3. Преимущества предварительно обученных моделей 

11.7. Предварительно обученные модели для трансферного обучения 

11.7.1. Трансферное обучение 
11.7.2. Процесс трансферного обучения 
11.7.3. Преимущества трансферного обучения 

11.8. Классификация и локализация в глубоком компьютерном зрении 

11.8.1. Классификация изображений 
11.8.2. Определение местоположения объектов на изображениях 
11.8.3. Обнаружение объектов 

11.9. Обнаружение объектов и их отслеживание 

11.9.1. Методы обнаружения объектов 
11.9.2. Алгоритмы отслеживания объектов 
11.9.3. Методы отслеживания и трассировки 

11.10. Семантическая сегментация 

11.10.1. Глубокое обучение для семантической сегментации 
11.10.2. Обнаружение краев 
11.10.3. Методы сегментации, основанные на правилах 

Модуль 12. Обработка естественного языка (NLP) с помощью естественных рекуррентных сетей (NNN) и внимания 

12.1. Генерация текста с использованием RNN 

12.1.1. Обучение RNN для генерации текста 
12.1.2. Генерация естественного языка с помощью RNN 
12.1.3. Приложения для генерации текста с помощью RNN 

12.2. Создание обучающего набора данных 

12.2.1. Подготовка данных для обучения RNN 
12.2.2. Хранение обучающего набора данных 
12.2.3. Очистка и преобразование данных 
12.2.4. Анализ настроений 

12.3. Ранжирование мнений с помощью RNN 

12.3.1. Выявление тем в комментариях 
12.3.2. Анализ настроений с помощью алгоритмов глубокого обучения 

12.4. Сеть кодирования-декодирования для нейронного машинного перевода 

12.4.1. Обучение RNN для машинного перевода 
12.4.2. Использование кодирующей-декодирующей сети для машинного перевода 
12.4.3. Повышение точности машинного перевода с помощью RNN 

12.5. Механизмы внимания 

12.5.1. Реализация механизмов внимания в RNN 
12.5.2. Использование механизмов внимания для повышения точности модели 
12.5.3. Преимущества механизмов внимания в нейронных сетях 

12.6. Модели трансформеров 

12.6.1. Использование моделей трансформеров для обработки естественного языка 
12.6.2. Применение моделей трансформеров для зрения 
12.6.3. Преимущества моделей трансформеров 

12.7. Трансформеры для зрения 

12.7.1. Применение моделей трансформеров для зрения 
12.7.2. Предварительная обработка данных изображений 
12.7.3. Обучение модели трансформеров для зрения 

12.8. Библиотека трансформеров Hugging Face 

12.8.1. Использование библиотеки трансформеров Hugging Face 
12.8.2. Применение библиотеки трансформеров Hugging Face 
12.8.3. Преимущества библиотеки трансформеров Hugging Face 

12.9. Другие библиотеки трансформеров. Сравнение 

12.9.1. Сравнение различных библиотек трансформеров 
12.9.2. Использование других библиотек трансформеров 
12.9.3. Преимущества других библиотек трансформеров 

12.10. Разработка NLP-приложения с использованием RNN и внимания. Практическое применение 

12.10.1. Разработка приложения для обработки естественного языка с использованием RNN и внимания 
12.10.2. Использование RNN, механизмов ухода и моделей трансформеров при внедрении 
12.10.3. Оценка практического применения 

Модуль 13. Автоэнкодеры, GAN и диффузионные модели 

13.1. Эффективные представления данных 

13.1.1. Снижение размерности 
13.1.2. Глубокое обучение 
13.1.3. Компактные представления 

13.2. Реализация РСА с неполным линейным автоматическим кодировщиком 

13.2.1. Процесс обучения 
13.2.2. Внедрение Python 
13.2.3. Использование тестовых данных 

13.3. Стековые автоматические кодировщики 

13.3.1. Глубокие нейронные сети 
13.3.2. Построение архитектур кодирования 
13.3.3. Использование инструментов 

13.4. Конволюционные автокодировщики 

13.4.1. Конструкция конволюционной модели 
13.4.2. Обучение конволюционной модели 
13.4.3. Оценка результатов 

13.5. Шумоподавление автоматических энкодеров 

13.5.1. Применение фильтров 
13.5.2. Проектирование моделей кодирования 
13.5.3. Использование методов регуляризации 

13.6. Автоматические разреженные автоматические энкодеры 

13.6.1. Повышение эффективности кодирования 
13.6.2. Минимизация числа параметров 
13.6.3. Применение методов регуляризации 

13.7. Автоматические вариационные энкодеры 

13.7.1. Использование вариационной оптимизации 
13.7.2. Глубокое обучение без контроля 
13.7.3. Глубокие латентные представления 

13.8. Генерация модных изображений MNIST 

13.8.1. Распознание паттернов 
13.8.2. Генерация изображений 
13.8.3. Обучение глубоких нейронных сетей 

13.9. Генеративные адверсарные сети и диффузионные модели 

13.9.1. Формирование контента из изображений 
13.9.2. Моделирование распределений данных 
13.9.3. Использование состязательных сетей 

13.10. Реализация моделей 

13.10.1. Практическое применение 
13.10.2. Реализация моделей 
13.10.3. Использование реальных данных 
13.10.4. Оценка результатов 

Модуль 14. Биоинспирированные алгоритмы

14.1. Введение в биоинспирированные алгоритмы 

14.1.1. Введение в биоинспирированные алгоритмы 

14.2. Алгоритмы социальной адаптации 

14.2.1. Биоинспирированные алгоритмы, основанные на муравьиных колониях 
14.2.2. Разновидности алгоритмов муравьиных колоний 
14.2.3. Алгоритмы, основанные на облаках с частицами 

14.3. Генетические алгоритмы 

14.3.1. Общая структура 
14.3.2. Внедрение основных операторов 

14.4. Стратегии освоения и использования пространства для генетических алгоритмов 

14.4.1. Алгоритм CHC 
14.4.2. Мультимодальные задачи 

14.5. Модели эволюционных вычислений (I) 

14.5.1. Эволюционные стратегии 
14.5.2. Эволюционное программирование 
14.5.3. Алгоритмы, основанные на дифференциальной эволюции 

14.6. Модели эволюционных вычислений (II) 

14.6.1. Модели эволюции, основанные на оценке алгоритмов распределения (EDA) 
14.6.2. Генетическое программирование 

14.7. Применение эволюционного программирования при нарушениях обучаемости 

14.7.1. Обучение на основе правил 
14.7.2. Эволюционные методы в задачах выбора экземпляра 

14.8. Многоцелевые задачи 

14.8.1. Концепция доминирования 
14.8.2. Применение эволюционных алгоритмов для решения многоцелевых задач 

14.9. Нейронные сети (I) 

14.9.1. Введение в нейронные сети 
14.9.2. Практический пример с нейронными сетями 

14.10. Нейронные сети (II) 

14.10.1. Примеры использования нейронных сетей в медицинских исследованиях 
14.10.2. Примеры использования нейронных сетей в экономике 
14.10.3. Примеры использования нейронных сетей в искусственном зрении 

Модуль 15. Искусственный интеллект: стратегии и применения

15.1. Финансовые услуги 

15.1.1. Последствия применения искусственного интеллекта (ИИ) в сфере финансовых услуг: возможности и проблемы
15.1.2. Примеры использования
15.1.3. Потенциальные риски, связанные с использованием ИИ 
15.1.4. Потенциальные будущие разработки/использования ИИ 

15.2. Последствия применения искусственного интеллекта в здравоохранении

15.2.1. Последствия ИИ в секторе здравоохранения. Возможности и проблемы
15.2.2. Примеры использования 

15.3. Риски, связанные с использованием ИИ в здравоохранении 

15.3.1. Потенциальные риски, связанные с использованием ИИ 
15.3.2. Потенциальные будущие разработки/использования ИИ

15.4. Розничная торговля

15.4.1. Последствия ИИ в розничной торговле. Возможности и проблемы
15.4.2. Примеры использования
15.4.3. Потенциальные риски, связанные с использованием ИИ
15.4.4. Потенциальные будущие разработки/использования ИИ 

15.5. Промышленность 

15.5.1. Последствия ИИ для промышленности. Возможности и проблемы 
15.5.2. Примеры использования 

15.6. Потенциальные риски, связанные с использованием ИИ в промышленности 

15.6.1. Примеры использования 
15.6.2. Потенциальные риски, связанные с использованием ИИ 
15.6.3. Потенциальные будущие разработки/использования ИИ

15.7. Государственное управление

15.7.1. Последствия использования искусственного интеллекта в государственном управлении. Возможности и проблемы 
15.7.2. Примеры использования
15.7.3. Потенциальные риски, связанные с использованием ИИ
15.7.4. Потенциальные будущие разработки/использования ИИ

15.8. Образовательная сфера

15.8.1. Последствия использования искусственного интеллекта в образовании. Возможности и проблемы 
15.8.2. Примеры использования
15.8.3. Потенциальные риски, связанные с использованием ИИ
15.8.4. Потенциальные будущие разработки/использования ИИ 

15.9. Лесное и сельское хозяйство

15.9.1. Последствия ИИ для лесного и сельского хозяйства. Возможности и проблемы
15.9.2. Примеры использования 
15.9.3. Потенциальные риски, связанные с использованием ИИ 
15.9.4. Потенциальные будущие разработки/использования ИИ

15.10. Кадровые ресурсы

15.10.1. Последствия ИИ для кадровых ресурсов. Возможности и проблемы 
15.10.2. Примеры использования
15.10.3. Потенциальные риски, связанные с использованием ИИ
15.10.4. Потенциальные будущие разработки/использования ИИ

Модуль 16. Диагностика в клинической практике с помощью ИИ 

16.1. Технологии и инструменты для диагностики с помощью ИИ 

16.1.1. Разработка программного обеспечения для диагностики с помощью ИИ в различных областях медицины 
16.1.2. Использование передовых алгоритмов для быстрого и точного анализа клинических признаков и симптомов 
16.1.3. Интеграция ИИ в диагностические приборы для повышения эффективности 
16.1.4. Инструменты ИИ для помощи в интерпретации результатов лабораторных тестов 

16.2. Интеграция мультимодальных клинических данных для диагностики 

16.2.1. Системы ИИ для объединения данных визуализации, лабораторных и клинических записей 
16.2.2. Инструменты для корреляции мультимодальных данных с целью постановки более точного диагноза 
16.2.3. Использование ИИ для анализа сложных закономерностей в различных типах клинических данных 
16.2.4. Интеграция геномных и молекулярных данных в диагностику с помощью ИИ 

16.3. Создание и анализ наборов данных о здоровье с помощью ИИ 

16.3.1. Создание клинических баз данных для обучения моделей ИИ 
16.3.2. Использование ИИ для анализа и извлечения информации из больших наборов данных по здравоохранению 
16.3.3. Инструменты ИИ для очистки и подготовки клинических данных 
16.3.4. Системы ИИ для выявления тенденций и закономерностей в медицинских данных 

16.4. Визуализация и управление медицинскими данными с помощью ИИ 

16.4.1. Инструменты ИИ для интерактивной и понятной визуализации данных о здоровье 
16.4.2. Системы ИИ для эффективного управления большими объемами клинических данных 
16.4.3. Использование приборных панелей на основе ИИ для мониторинга показателей здоровья 
16.4.4. Технологии ИИ для управления и обеспечения безопасности медицинских данных 

16.5. Распознавание паттернов и машинное обучение в клинической диагностике 

16.5.1. Применение методов машинного обучения для распознавания паттернов в клинических данныхpara el reconocimiento de patrones en datos clínicos 
16.5.2. Использование ИИ для раннего выявления заболеваний с помощью анализа моделей 
16.5.3. Разработка прогностических моделей для более точной диагностики 
16.5.4. Внедрение алгоритмов машинного обучения для интерпретации данных о здоровье 

16.6. Интерпретация медицинских изображений с помощью ИИ 

16.6.1. Системы ИИ для обнаружения и классификации аномалий на медицинских изображениях 
16.6.2. Использование глубокого обучения в интерпретации рентгеновских снимков, МРТ и КТ 
16.6.3. Инструменты ИИ для повышения точности и скорости диагностической визуализации 
16.6.4. Внедрение ИИ для поддержки принятия клинических решений на основе изображений 

16.7. Обработка естественного языка в медицинских записях для постановки клинического диагноза 

16.7.1. Использование PNL для извлечения необходимой информации из медицинской документации 
16.7.2. Системы ИИ для анализа записей врачей и отчетов пациентов 
16.7.3. Инструменты ИИ для обобщения и классификации информации из медицинской документации 
16.7.4. Применение PNL для идентификации симптомов и диагнозов из клинических текстов 

16.8. Валидация и оценка диагностических моделей с помощью ИИ 

16.8.1. Методы валидации и тестирования моделей ИИ в реальных клинических условиях 
16.8.2. Оценка производительности и точности диагностических инструментов с помощью ИИ 
16.8.3. Использование ИИ для обеспечения надежности и этичности клинической диагностики 
16.8.4. Внедрение протоколов непрерывной оценки систем ИИ в здравоохранении 

16.9. ИИ в диагностике редких заболеваний 

16.9.1. Разработка специализированных систем ИИ для выявления редких заболеваний 
16.9.2. Использование ИИ для анализа нетипичных паттернов и сложной симптоматики 
16.9.3. Инструменты ИИ для ранней и точной диагностики редких заболеваний 
16.9.4. Внедрение глобальных баз данных с использованием ИИ для улучшения диагностики редких заболеваний 

16.10. Истории успеха и проблемы при внедрении диагностики с помощью ИИ 

16.10.1. Анализ конкретных примеров, когда ИИ значительно улучшил клиническую диагностику 
16.10.2. Оценка проблем, связанных с внедрением ИИ в клинических условиях 
16.10.3. Обсуждение этических и практических барьеров на пути внедрения ИИ для диагностики 
16.10.4. Изучение стратегий преодоления барьеров на пути интеграции ИИ в медицинскую диагностику 

Модуль 17. Лечение и ведение пациента с ИИ 

17.1. Системы лечения с помощью ИИ 

17.1.1. Разработка систем ИИ для помощи в принятии терапевтических решений 
17.1.2. Использование ИИ для персонализации лечения на основе индивидуальных профилей 
17.1.3. Внедрение средств ИИ при назначении дозировок и графиков приема лекарств 
17.1.4. Интеграция ИИ в мониторинг и корректировку лечения в режиме реального времени 

17.2. Определение показателей для контроля состояния здоровья пациента 

17.2.1. Определение ключевых параметров с помощью ИИ для мониторинга состояния здоровья пациента 
17.2.2. Использование ИИ для определения прогностических показателей здоровья и болезней 
17.2.3. Разработка систем раннего предупреждения на основе показателей здоровья 
17.2.4. Внедрение ИИ для непрерывной оценки состояния здоровья пациентов 

17.3. Инструменты для мониторинга и контроля показателей здоровья 

17.3.1. Разработка мобильных и носимых приложений для мониторинга здоровья с поддержкой ИИ 
17.3.2. Внедрение систем ИИ для анализа медицинских данных в режиме реального времени 
17.3.3. Использование приборных панелей на основе ИИ для визуализации и мониторинга показателей здоровья 
17.3.4. Интеграция IoT-устройств в непрерывный мониторинг показателей здоровья с помощью ИИ 

17.4. ИИ в планировании и проведении медицинских процедур 

17.4.1. Использование систем искусственного интеллекта для оптимизации планирования операций и медицинских процедур 
17.4.2. Внедрение ИИ в симуляцию и практику хирургических процедур 
17.4.3. Использование ИИ для повышения точности и эффективности выполнения медицинских процедур 
17.4.4. Применение ИИ в координации и управлении хирургическими ресурсами 

17.5. Алгоритмы машинного обучения для создания терапевтического лечения 

17.5.1. Использование машинного обучения для разработки персонализированных протоколов лечения 
17.5.2. Внедрение предиктивных алгоритмов для выбора эффективных методов лечения 
17.5.3. Разработка систем ИИ для адаптации лечения в режиме реального времени 
17.5.4. Применение ИИ для анализа эффективности различных вариантов терапии 

17.6. Адаптивность и постоянное обновление терапевтических протоколов с помощью ИИ 

17.6.1. Внедрение систем ИИ для динамического пересмотра и обновления методов лечения 
17.6.2. Использование ИИ для адаптации терапевтических протоколов к новым результатам и данным 
17.6.3. Разработка инструментов ИИ для непрерывной персонализации лечения 
17.6.4. Интеграция ИИ в адаптивную реакцию на изменяющиеся состояния пациентов 

17.7. Оптимизация медицинских услуг с помощью технологий ИИ 

17.7.1. Использование ИИ для повышения эффективности и качества медицинских услуг 
17.7.2. Внедрение систем искусственного интеллекта для управления ресурсами здравоохранения 
17.7.3. Разработка инструментов искусственного интеллекта для оптимизации рабочего процесса в больницах 
17.7.4. Применение ИИ для сокращения времени ожидания и улучшения качества обслуживания пациентов 

17.8. Применение ИИ для реагирования на чрезвычайные ситуации в здравоохранении 

17.8.1. Внедрение систем ИИ для быстрого и эффективного управления кризисными ситуациями в здравоохранении 
17.8.2. Использование ИИ для оптимизации распределения ресурсов в чрезвычайных ситуациях 
17.8.3. Разработка инструментов ИИ для прогнозирования вспышек заболеваний и реагирования на них 
17.8.4. Интеграция ИИ в системы оповещения и связи во время чрезвычайных ситуаций в области здравоохранения 

17.9. Междисциплинарное сотрудничество в области лечения с помощью ИИ 

17.9.1. Поощрение сотрудничества между различными медицинскими специальностями с использованием систем ИИ 
17.9.2. Использование ИИ для интеграции знаний и навыков из различных дисциплин в процессе лечения 
17.9.3. Разработка платформ ИИ для облегчения междисциплинарной коммуникации и координации 
17.9.4. Внедрение ИИ при создании междисциплинарных лечебных групп 

17.10. Успешный опыт применения ИИ в лечении заболеваний 

17.10.1. Анализ историй успеха в использовании ИИ для эффективного лечения заболеваний 
17.10.2. Оценка влияния ИИ на улучшение результатов лечения 
17.10.3. Документирование инновационного опыта использования ИИ в различных областях медицины 
17.10.4. Обсуждение достижений и проблем, связанных с внедрением ИИ в медицинскую практику 

Модуль 18. Персонализация здоровья с помощью ИИ 

18.1. Применение ИИ в геномике для персонализированной медицины 

18.1.1. Разработка алгоритмов ИИ для анализа генетических последовательностей и их связи с заболеваниями 
18.1.2. Использование ИИ для определения генетических маркеров для персонализированного лечения 
18.1.3. Внедрение ИИ для быстрой и точной интерпретации геномных данных 
18.1.4. Инструменты ИИ для корреляции генотипов с реакцией на лекарства 

18.2. ИИ в фармакогеномике и разработке лекарств 

18.2.1. Разработка моделей ИИ для прогнозирования эффективности и безопасности лекарств 
18.2.2. Использование ИИ для идентификации терапевтических мишеней и разработки лекарств 
18.2.3. Применение ИИ в анализе взаимодействия генов и лекарств для персонализации лечения 
18.2.4. Внедрение алгоритмов ИИ для ускорения открытия новых лекарств 

18.3. Персонализированный мониторинг с помощью интеллектуальных устройств и ИИ 

18.3.1. Разработка носимых устройств с ИИ для непрерывного мониторинга показателей здоровья 
18.3.2. Использование ИИ для интерпретации данных, собранных смарт-устройствами 
18.3.3. Внедрение систем раннего предупреждения заболеваний на основе ИИ 
18.3.4. Инструменты ИИ для персонализации рекомендаций по образу жизни и здоровью 

18.4. Системы поддержки принятия клинических решений с помощью ИИ 

18.4.1. Внедрение ИИ для помощи врачам в принятии клинических решений 
18.4.2. Разработка систем ИИ, предоставляющих рекомендации на основе клинических данных 
18.4.3. Использование ИИ для оценки риска/пользы различных вариантов терапии 
18.4.4. Инструменты ИИ для интеграции и анализа медицинских данных в режиме реального времени 

18.5. Тенденции персонализации здоровья с помощью ИИ 

18.5.1. Анализ последних тенденций в области ИИ для персонализации здравоохранения 
18.5.2. Использование ИИ для разработки профилактических и прогностических подходов в здравоохранении 
18.5.3. Внедрение ИИ для адаптации медицинских планов к индивидуальным потребностям 
18.5.4. Изучение новых технологий ИИ в области персонализированного здравоохранения 

18.6. Достижения в области хирургической робототехники с использованием ИИ 

18.6.1. Разработка хирургических роботов с ИИ для точных, минимально инвазивных процедур 
18.6.2. Использование ИИ для повышения точности и безопасности роботизированной хирургии 
18.6.3. Внедрение систем ИИ для хирургического планирования и моделирования операций 
18.6.4. Достижения в области интеграции тактильной и визуальной обратной связи в хирургической робототехнике с использованием ИИ 

18.7. Разработка прогностических моделей для персонализированной клинической практики 

18.7.1. Использование ИИ для создания прогностических моделей заболеваний на основе индивидуальных данных 
18.7.2. Применение ИИ для прогнозирования ответа на лечение 
18.7.3. Разработка инструментов ИИ для прогнозирования рисков для здоровья 
18.7.4. Применение прогностического моделирования при планировании профилактических мероприятий 

18.8. ИИ в персонализированном обезболивании и лечении 

18.8.1. Разработка систем ИИ для оценки и персонализированного лечения боли 
18.8.2. Использование ИИ для выявления моделей боли и реакции на лечение 
18.8.3. Внедрение инструментов ИИ в персонализацию терапии боли 
18.8.4. Применение ИИ для мониторинга и корректировки планов лечения боли 

18.9. Автономия пациента и активное вовлечение в персонализацию 

18.9.1. Продвижение самостоятельности пациентов с помощью средств ИИ для управления их медицинским обслуживанием 
18.9.2. Разработка систем ИИ, расширяющих возможности пациентов в принятии решений 
18.9.3. Использование ИИ для предоставления персонализированной информации и обучения пациентов 
18.9.4. Инструменты ИИ, способствующие активному участию пациентов в лечении 

18.10. Интеграция ИИ в электронные медицинские карты 

18.10.1. Внедрение ИИ для эффективного анализа и управления электронными медицинскими записями 
18.10.2. Разработка инструментов ИИ для извлечения клинических данных из электронных записей 
18.10.3. Использование ИИ для повышения точности и доступности данных в медицинских картах 
18.10.4. Применение ИИ для соотнесения данных медицинской карты с планами лечения 

Модуль 19. Анализ больших данных в секторе здравоохранения с помощью ИИ 

19.1. Основы больших данных в здравоохранении 

19.1.1. Бурный рост объема данных в секторе здравоохранения 
19.1.2. Концепция больших данных и основные инструменты 
19.1.3. Применение больших данных в здравоохранении 

19.2. Обработка и анализ текста в медицинских данных 

19.2.1. Концепции обработки естественного языка 
19.2.2. Методы embeding 
19.2.3. Применение обработки естественного языка в здравоохранении 

19.3. Передовые методы поиска данных в здравоохранении 

19.3.1. Исследование инновационных методов для эффективного поиска данных в здравоохранении 
19.3.2. Разработка передовых стратегий для извлечения и организации информации в медицинских учреждениях 
19.3.3. Внедрение адаптивных и специализированных методов поиска данных для различных клинических условий 

19.4. Оценка качества при анализе медицинских данных 

19.4.1. Разработка показателей для тщательной оценки качества данных в медицинских учреждениях 
19.4.2. Внедрение инструментов и протоколов для обеспечения качества данных, используемых в клиническом анализе 
19.4.3. Постоянная оценка точности и надежности результатов в проектах по анализу медицинских данных 

19.5. Добыча данных и машинное обучение в здравоохранении 

19.5.1. Основные методологии интеллектуального анализа данных 
19.5.2. Интеграция данных о здоровье 
19.5.3. Выявление закономерностей и аномалий в медицинских данных 

19.6. Инновационные направления использования больших данных и ИИ в здравоохранении 

19.6.1. Исследование новых рубежей в применении больших данных и ИИ для преобразования сектора здравоохранения 
19.6.2. Выявление инновационных возможностей для интеграции технологий больших данных и ИИ в медицинскую практику 
19.6.3. Разработка передовых подходов для максимального использования потенциала больших данных и ИИ в секторе здравоохранения 

19.7. Сбор и предварительная обработка медицинских данных 

19.7.1. Разработка эффективных методик сбора медицинских данных в клинических и исследовательских условиях 
19.7.2. Внедрение передовых методов предварительной обработки для оптимизации качества и полезности медицинских данных 
19.7.3. Разработка стратегий сбора и предварительной обработки, обеспечивающих конфиденциальность и неприкосновенность медицинской информации 

19.8. Визуализация данных и коммуникация в здравоохранении 

19.8.1. Разработка инновационных средств визуализации в здравоохранении 
19.8.2. Креативные стратегии коммуникации в сфере здравоохранения 
19.8.3. Интеграция интерактивных технологий в здравоохранение 

19.9. Безопасность и управление данными в секторе здравоохранения 

19.9.1. Разработка комплексных стратегий безопасности данных для защиты конфиденциальности и неприкосновенности частной жизни в секторе здравоохранения 
19.9.2. Внедрение эффективных механизмов управления для обеспечения этичного и ответственного управления данными в медицинских учреждениях 
19.9.3. Разработка политики и процедур для обеспечения целостности и доступности медицинских данных с учетом проблем, характерных для сектора здравоохранения 

19.10. Практическое применение больших данных в здравоохранении 

19.10.1. Разработка специализированных решений для управления и анализа больших массивов данных в сфере здравоохранения 
19.10.2. Использование практических инструментов на основе больших данных для поддержки принятия клинических решений 
19.10.3. Применение инновационных подходов к большим данным для решения конкретных задач в секторе здравоохранения 

Модуль 20. Этика и регулирование в медицинском искусственном интеллекте 

20.1. Этические принципы применения ИИ в медицине 

20.1.1. Анализ и принятие этических принципов при разработке и использовании систем медицинского ИИ 
20.1.2. Интеграция этических ценностей в процесс принятия решений с помощью ИИ в медицинских контекстах 
20.1.3. Разработка этических принципов для обеспечения ответственного использования искусственного интеллекта в медицине 

20.2. Конфиденциальность данных и согласие в медицинских контекстах 

20.2.1. Разработка политик конфиденциальности для защиты конфиденциальных данных в медицинских приложениях ИИ 
20.2.2. Обеспечение информированного согласия при сборе и использовании персональных данных в медицинской сфере 
20.2.3. Реализация мер безопасности для защиты частной жизни пациентов в медицинских ИИ-средах 

20.3. Этика в исследованиях и разработке систем медицинского ИИ 

20.3.1. Этическая оценка исследовательских протоколов при разработке систем медицинского ИИ 
20.3.2. Обеспечение прозрачности и этической строгости на этапах разработки и валидации систем медицинского ИИ 
20.3.3. Этические соображения при публикации и распространении результатов в области медицинского ИИ 

20.4. Социальное воздействие и ответственность в ИИ для здравоохранения 

20.4.1. Анализ социального воздействия ИИ на оказание медицинских услуг 
20.4.2. Разработка стратегий снижения рисков и этической ответственности при применении ИИ в медицине 
20.4.3. Постоянная оценка социального воздействия и адаптация систем ИИ для внесения позитивного вклада в общественное здравоохранение 

20.5. Устойчивое развитие ИИ в секторе здравоохранения 

20.5.1. Интеграция устойчивых практик в разработку и обслуживание систем здравоохранения ИИ 
20.5.2. Оценка экологического и экономического воздействия технологий ИИ в секторе здравоохранения 
20.5.3. Разработка устойчивых бизнес-моделей для обеспечения непрерывности и совершенствования решений ИИ в секторе здравоохранения 

20.6. Управление данными и международная нормативная база в медицинском ИИ 

20.6.1. Разработка рамок управления для этичного и эффективного управления данными в медицинских приложениях ИИ 
20.6.2. Адаптация к международным стандартам и нормам для обеспечения соблюдения этических и правовых норм 
20.6.3. Активное участие в международных инициативах по установлению этических стандартов при разработке систем медицинского ИИ 

20.7. Экономические аспекты ИИ в секторе здравоохранения 

20.7.1. Анализ экономических последствий и затрат при внедрении систем ИИ в здравоохранении 
20.7.2. Разработка бизнес-моделей и финансирования для содействия внедрению технологий ИИ в секторе здравоохранения 
20.7.3. Оценка экономической эффективности и справедливости доступа к медицинским услугам, управляемым ИИ 

20.8. Разработка систем медицинского ИИ, ориентированных на человека 

20.8.1. Интеграция принципов дизайна, ориентированного на человека, для повышения удобства использования и приемлемости систем медицинского ИИ 
20.8.2. Вовлечение медицинских работников и пациентов в процесс разработки, чтобы обеспечить актуальность и эффективность решений 
20.8.3. Постоянная оценка пользовательского опыта и обратной связи для оптимизации взаимодействия с системами ИИ в медицинских учреждениях 

20.9. Справедливость и прозрачность в машинном обучении в медицине 

20.9.1. Разработка моделей машинного обучения в медицине, способствующих справедливости и прозрачности 
20.9.2. Внедрение практик для смягчения предвзятости и обеспечения справедливости при применении алгоритмов ИИ в секторе здравоохранения 
20.9.3. Постоянная оценка справедливости и прозрачности при разработке и внедрении решений машинного обучения в медицине 

20.10. Безопасность и политика при внедрении ИИ в медицину 

20.10.1. Разработка политик безопасности для защиты целостности и конфиденциальности данных в применениях медицинского ИИ 
20.10.2. Реализация мер безопасности при развертывании систем ИИ для предотвращения рисков и обеспечения безопасности пациентов 
20.10.3. Постоянная оценка политики безопасности для адаптации к технологическому прогрессу и новым проблемам при внедрении медицинского ИИ 

Воспользуйтесь возможностью узнать о последних достижениях в этой области и применить их в своей повседневной практике"